最优化 Optimization
最优化就是通过计算权重\(W\)来最小化损失函数。如果损失函数是SVM损失,那么这个凸函数是可以用凸优化的方法进行的。但是当损失函数扩展成为神经网络时,那么目标函数就不是凸函数了,而且损失函数中存在不可导点(kinks),使得这些点不可微,在这些点也没有梯度的定义。但是次梯度(subgradient)依然可以使用。
我们从最基本的方案开始逐步过渡到梯度的方法。
随机搜索
大量随机生成权重矩阵,然后比较它们的损失值,取最小的权重作为我们要找的权重去跑测试集。
# 假设X_train的每一列都是一个数据样本(比如3073 x 50000)
# 假设Y_train是数据样本的类别标签(比如一个长50000的一维数组)
# 假设函数L对损失函数进行评价
bestloss = float("inf") # Python assigns the highest possible float value
for num in xrange(1000):
W = np.random.randn(10, 3073) * 0.0001 # generate random parameters
loss = L(X_train, Y_train, W) # get the loss over the entire training set
if loss < bestloss: # keep track of the best solution
bestloss = loss
bestW = W
print 'in attempt %d the loss was %f, best %f' % (num, loss, bestloss)
# 测试函数
# 假设X_test尺寸是[3073 x 10000], Y_test尺寸是[10000 x 1]
scores = Wbest.dot(Xte_cols) # 10 x 10000, the class scores for all test examples
# 找到在每列中评分值最大的索引(即预测的分类)
Yte_predict = np.argmax(scores, axis = 0)
# 以及计算准确率
np.mean(Yte_predict == Yte)
# 返回 0.1555当随机猜测时,正确概率是10%,这里用多次筛选得到随机矩阵提升了一点。如果我们能够设计一个迭代算法,使得每次迭代后的损失值都减少一点,那么就能找到更好的\(W\)。
随机本地搜索
设计一个迭代算法,每一次都随机尝试几个方向,如果方向是向下(能让损失值小一点),那就向该方向走一步。依然从随机的\(W\)开始,每次给予一个随机扰动\(\delta W\),如果扰动后损失值更小了,就更新权重矩阵。
W = np.random.randn(10, 3073) * 0.001 # 生成随机初始W
bestloss = float("inf")
for i in xrange(1000):
step_size = 0.0001
Wtry = W + np.random.randn(10, 3073) * step_size
loss = L(Xtr_cols, Ytr, Wtry)
if loss < bestloss:
W = Wtry
bestloss = loss
print 'iter %d loss is %f' % (i, bestloss)用同样的方法,相比上述方法准确率更高(20%),但是因为迭代过程是随机的,所以训练时间和效果都不稳定。
跟随梯度
这里的迭代算法保证了每次都是走向局部最优的低处,这个方向就是损失函数的梯度(gradient)。梯度是各个维度的斜率组成的向量(导数derivatives)。当函数有多个参数时,梯度是每个维度上偏导数所形成的向量。
梯度计算
计算梯度的方法有两种:数值梯度法(近似),分析梯度法(精确,需要微分)。
- 有限差值法近似求梯度
用梯度公式\(\frac{f(x+h)-f(x)}{h}\)在所有维度上进行计算,得到的grad中包括了在每个维度上的偏导数。h的取值越小越好,实际中使用中心差值公式(centered difference formula,对称差分中一次项误差相消)会更好,公式为\(\frac{[f(x+h)-f(x-h)]}{2h}\)。以下函数是根据输入函数与向量计算函数梯度的函数:
def eval_numerical_gradient(f, x):
"""
一个f在x处的数值梯度法的简单实现
- f是只有一个参数的函数
- x是计算梯度的点
"""
fx = f(x) # 在原点计算函数值
grad = np.zeros(x.shape)
h = 0.00001
# 对x中所有的索引进行迭代
it = np.nditer(x, flags=['multi_index'], op_flags=['readwrite'])
while not it.finished:
# 计算x+h处的函数值
ix = it.multi_index
old_value = x[ix]
x[ix] = old_value + h # 增加h
fxh = f(x) # 计算f(x + h)
x[ix] = old_value # 存到前一个值中 (非常重要)
# 计算偏导数
grad[ix] = (fxh - fx) / h # 坡度
it.iternext() # 到下个维度
return grad
# 要使用上面的代码我们需要一个只有一个参数的函数
# (在这里参数就是权重)所以也包含了X_train和Y_train
def CIFAR10_loss_fun(W):
return L(X_train, Y_train, W)
W = np.random.rand(10, 3073) * 0.001 # 随机权重向量
df = eval_numerical_gradient(CIFAR10_loss_fun, W) # 得到梯度
# 用得到的梯度更新权重
loss_original = CIFAR10_loss_fun(W) # 初始损失值
print 'original loss: %f' % (loss_original, )
# 查看不同步长的效果
for step_size_log in [-10, -9, -8, -7, -6, -5,-4,-3,-2,-1]:
step_size = 10 ** step_size_log
W_new = W - step_size * df # 权重空间中的新位置
loss_new = CIFAR10_loss_fun(W_new)
print 'for step size %f new loss: %f' % (step_size, loss_new)通过这个函数可以计算任何函数在任意点上的梯度,并用于更新权重。这里是向着梯度的负方向进行更新,因为我们希望损失函数值是降低的。在这个计算过程中,学习步长是关键的超参数(学习率),过大的步长会导致更高的损失值。
使用数值近似的方法每一步要计算N维权值矩阵的每一个梯度,当神经网络中参数众多时,这个方法将不再适合。
- 微分分析法
用微分的方法得到损失函数的梯度公式,不好的地方在于容易出错。所以在实际应用时,会将分析梯度法与数值梯度法结果比较,来检查微分分析的正确性,这个步骤叫做梯度检查。
这里将SVM损失函数进行微分:
\(L_i=\sum_{j \neq y_i}[max(0,w_j^T x_i-w_{y_i}^T x_i+\Delta)]\) \(\bigtriangledown_{w_{y_i}} L_i=-(\sum_{j \neq y_i}\mathbb{I}(w_j^T x_i-w_{y_i}^T x_i+\Delta>0))x_i\)
其中的\(\mathbb{I}\)是一个示性函数,若括号中条件为真则函数值为1,否则为0。这里的微分公式非常简单,不满足条件的分类乘以\(x_i\)就是梯度了。这里的梯度对应正确分类的权值矩阵行向量梯度,其他行的梯度为:
\[\bigtriangledown_{w_{y_i}} L_i=\mathbb{I}(w_j^T x_i-w_{y_i}^T x_i+\Delta>0)x_i\]梯度下降
得到损失函数的梯度后就可以进行梯度下降的过程。普通的梯度下降法只适用于小数据量,在大数据量下,计算整个数据集来获取一个参数的代价过高,常用方法是计算训练集中的小批量(batches)数据。因为训练集中的数据大多相关,通过小批量数据梯度计算可以实现快速收敛,以此进行更频繁地更新。
当每个批量中只有一个数据样本时,这种策略被称为随机梯度下降(Stochastic Gradient Descent, SGD)。一般来说,小批量数据的大小一般使用2的指数,因为它由存储器限制,输入是2的倍数时运算会大大加快。
# 普通的梯度下降
while True:
weights_grad = evaluate_gradient(loss_fun, data, weights)
weights += - step_size * weights_grad # 进行梯度更新
# 普通的小批量数据梯度下降
while True:
data_batch = sample_training_data(data, 256) # 256个数据
weights_grad = evaluate_gradient(loss_fun, data_batch, weights)
weights += - step_size * weights_grad # 参数更新最优化是为了解决损失函数最小时权重矩阵如何得到的问题,也就是求参的问题。当损失函数为凸函数可以使用凸优化,而当不可微点多或非凸函数时,则要使用梯度下降的方法求局部最优,有时近似法也要用来进行梯度检查。
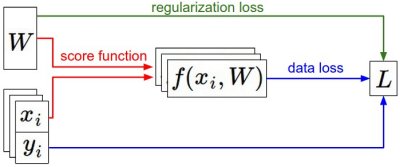
后面我将继续学习反向传播(backpropagation)机制,它使用链式法则来高效计算梯度,能够对包含CNN在内的大多数神经网络的损失函数进行最优化。
